Mathematik: Seevermessung wie bei den Sumerern
Von Johannes Dippel (CJD-Update, 10e)
 Pilotversuch: Gymnasiasten unterziehen sich
Pilotversuch: Gymnasiasten unterziehen sich
schriftlicher Realschulprüfung
In den letzten Wochen des Schuljahres stand bei der 10e in Mathematik hauptsächlich Wiederholung auf dem Programm. Dazu gehörte auch das Absolvieren der aktuellen Realschul-Abschlussarbeit 2006. Ein wichtiges Thema der Klasse 10 war Trigonometrie, also Dreiecksberechnung. Als eine praktische Anwendung erhielten wir die Aufgabe, mit einer simplen Wäscheleine die Länge des Oberurffer Sees zu ermitteln. Nach kurzer Lagebesprechung im Team war der Lösungsansatz klar: DIE Formeln der Trigonometrie sind anzuwenden, mit deren Hilfe man aus einer Seite und einem Winkel die gesuchte Seite berechnen kann. Die Klasse zog danach zum See. Dort angekommen wurde die Länge der Leine bestimmt. Als Messgerät musste der Turnschuh von Max hinhalten. Dann wurde die Leine zwischen zwei Bäumen gespannt und ein Fahnenmast als Peilpunkt am anderen Seeufer festgelegt.
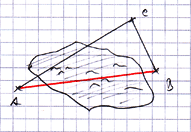
Mit dem Geodreieck ließen sich die von Wäscheleine und Peilstrecken gebildeten Winkel bequem messen. Dieses Verfahren ist schon über 5.000 Jahre alt. Es wurde beispielsweise bereits von den alten Sumerern angewandt. In der nächsten Mathematikstunde hat Nura in einem gelungenen Referat die Berechnung der Seelänge anhand der Messdaten vorgeführt. Ungefähr 55 Meter! Dieses praxisbezogene Beispiel zeigt, dass man mit einfachsten Mitteln und etwas mathematischem Wissen große Entfernungen genau berechnen kann, ohne sich groß von der Stelle zu bewegen.
(Bild/Gestaltung: A. Bubrowski)
Kommentare