Abb. 1

1. Schwingung einer Stimmgabel

Direkt vor dem Resonanzkörper einer Stimmgabel z.B. des Kammertons a’ steht das Messmikrofon, das über das CBL 2 an den Taschencomputer TI 89 oder Voyage 200 angeschlossen ist (Abb.1). Die Grundeinstellungen des Messprogramms „datamate“ können nach automatischem Erkennen des Mikrofons als Sensor direkt übernommen werden.

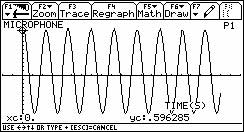
Man schlägt die Stimmgabel an und startet die Aufnahme der Messung.

Es erscheint nach kurzer Berechnungszeit ein Oszillogramm der sinusförmigen Schwingung der Stimmgabel (Abb.2 – links).

Der hier eingeblendete y-Wert ist die Amplitude der Schwingung abhängig von der Lautstärke des angeschlagenen Tons. Da das Auswertungsprogramm automatisch die y-Skalierung anpasst, lässt sich die Stärke der Amplitude nur über den Cursor bestimmen.

Wenn man eine andere sinusförmige Schallquelle benutzt und dabei auch eine andere Frequenz benutzt, verändert sich im Vergleich zu Abb.2 die Anzahl der Perioden auf dem Display.

Abb. 3 – 5

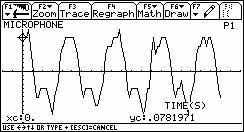
2. Klangfarbe von Musikinstrumenten

Wird zum Beispiel der Kammerton a’ (Frequenz f = 440 Hz) von einer Violine und einer Querflöte gespielt, so empfindet das menschliche Ohr den gleichen Ton recht unterschiedlich: einerseits der zarte Ton der Violine und andererseits der schrille Ton der Querflöte. Der Musiker spricht hier von der „Klangfarbe“ eines Instruments, der Überlagerung von Grund- und Oberschwingungen.

Betrachten wir zunächst den physikalischen Hintergrund. Auf dem Wellenträger (Saite eines Klaviers oder einer Geige, Luftsäule in einer Flöte oder Orgelpfeife) bilden sich stehende Wellen aus.

Bei einer eingespannten Saite hat man zwei feste Enden. Somit gilt für das Frequenzverhältnis der entstehenden Grund- und Oberschwingungen:

f0 : f1 : f2 : … : fn = 1 : 2 : 3 : … : (n+1)

Das gleiche Frequenzverhältnis erhält man, wenn die beiden Enden des Wellenträgers lose sind. Bei einigen Blasinstrumenten (z.B. Oboe, Klarinette, Saxophon) haben wir es mit einem festen und einem losen Ende des Wellenträgers zu tun. Hier gilt für das Verhältnis der Frequenzen von Grund- und Oberschwingungen:

f0 : f1 : f2 : … : fn = 1 : 3 : 5 : … : (2n+1)

Mit Hilfe von CBL und Messmikrofon kann die Klangfarbe eines Musikinstruments untersucht werden. Statt einer Stimmgabel nimmt man ein Musikinstrument. Als Beispiele sind hier in den beiden Abbildungen die Oszillogramme einer Altflöte (Abb.3), einer Posaune (Abb.4) und einer Orgelpfeife (Abb.5) dargestellt. Damit im Oszillogramm die Obertöne besser zu erkennen sind, wurde in den drei Abbildungen die Zeitachse mit dem Faktor 2 gestreckt. Man erkennt in den Abweichungen zur sinusförmigen Schwingung der Stimmgabel die Existenz von Oberschwingungen.

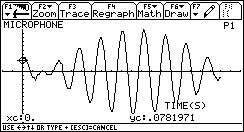
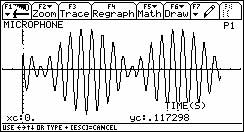Abb. 6 und 7

3. Schwebung

Im nächsten Versuch steht dicht neben der Stimmgabel noch ein Tonfrequenzgenerator. Die dort eingestellte Frequenz muss relativ stark von 440 Hz abweichen. Es eignet sich eine Frequenz von 500Hz. Wenn man die Voreinstellungen des Messprogramms einbehält, erhält man genau eine Schwebung (Abb.6). Wählt man im Messprogramm TIME GRAPH-0.04, so werden zwei Schwebungen dargestellt (Abb.7).

4. Weitere mögliche Experimente

In den obigen Experimenten wurden sinusförmige Schwingungen und deren Überlagerungen betrachtet.

Abb. 8

Etwas schwieriger ist es, z.B. einen Knall aufzunehmen. Reflexionen an Wänden oder am Experimentiertisch können das ursprüngliche Signal überlagern und somit das Oszillogramm verfälschen. Wichtig ist deshalb, z.B. durch Abschirmung des Mikrofons oder Abdeckung des Tisches mit einer Wolldecke solche Reflexionen zu unterdrücken. Das Bild eines Knalls hat dann Aussehen wie in Abb. 8.

Abb. 9

Einen Knall kann man auch ausnutzen zur Bestimmung der Schallgeschwindigkeit in Luft. Dazu stellt man vor die Öffnung eines einseitig geschlossenen Rohrs (Durchmesser ca. 10 cm, Länge mindestens 1,50 m) (Abb.9).

Die Messung hier erfolgte triggergesteuert. Der in das Rohr laufende Knall löste die Messung aus. Die Laufzeit des Schalls kann ausgemessen werden.

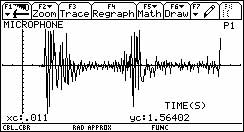
Sie beträgt in diesem Beispiel 0,0087 s bei einem Abstand vom Mikrofon zum geschlossenen Ende des Rohrs von 1,50 m. Damit erhält man eine Schallgeschwindigkeit c = 345 m/s. (siehe Abb. 10, rechts).

5. Anmerkung

Zehn physikalische Simulationen ohne Messonden mit dem Voyage 200 sind veröffentlicht auf der Materialienseite von Texas Instruments und bei www.t3deutschland.de. Das Download ist jeweils kostenlos.

Weitere Simulationen zur Mathematik und Physik sowie physikalische Experimente mit Messonden (Ziegenproblem, Wappen oder Zahl, Würfeln, Werfen von Reißzwecken, Programmpaket zur Trigonometrie, Kurvendiskussion, genaue Beschreibung der obigen Versuche mit dem Mikrofon, Induktion einer Spule) sind auf Anfrage erhältlich: rupeiffer@t-online.de.